Code Complexity and Python
This took way more time than I thought…
When I decided to change jobs in 2021, I realized that my experience till that point was restricted to data analysis. I wanted to keep working with Python but could not just rely on data, so I decided to study Python in a more software-developer way.
It happens that when you are studying alone, things get hard. Like, when you’re in school everything is kind of tailored for you. On your own… things get complicated. The internet has too much information and every tab you open gets you to an ocean of information.
In one of these sailings to gather knowledge I stumbled across this super famous book that I never heard of: Cracking the Code Interview. And in case you also didn’t know about it, the book consists of 189 (yeah) programming questions from tech interviews. The chapters introduce the topic to be approached and the solutions.
Basic and straight to the business. So I bought it 😃
I opened it when it arrived and started to study right away. I was so excited that I made myself accountable by creating a repo with the solutions to these exercises.
So far I finished chapter One, which I’ll write about in a future post (stay tuned!). But! I did learn some cool stuff that I’ll share with you now.
So, in this post, I’m going to share something that a bunch of people already talked about, but I didn’t: Big-O! And in case you never heard of it I’m honored to be the first to introduce you to this topic 🥳
Let’s dive in!
Big-O
Big-O is a mathematical notation invented by Paul Bachman and Edmund Landau to describe the limits of a function. When we apply it to computer science we are measuring the efficiency of a code when the size of the input increases, e.g., how scalable a routine can be.
That means that if you have a function that prints out an array of n values it will take O(n) time to do so. Increase the number of values inside that array and you can have O(n²), O(n!), or any other big O times. This sets the upper boundary or the worst-case scenario you could have.
The graph below shows the most common runtimes possible.
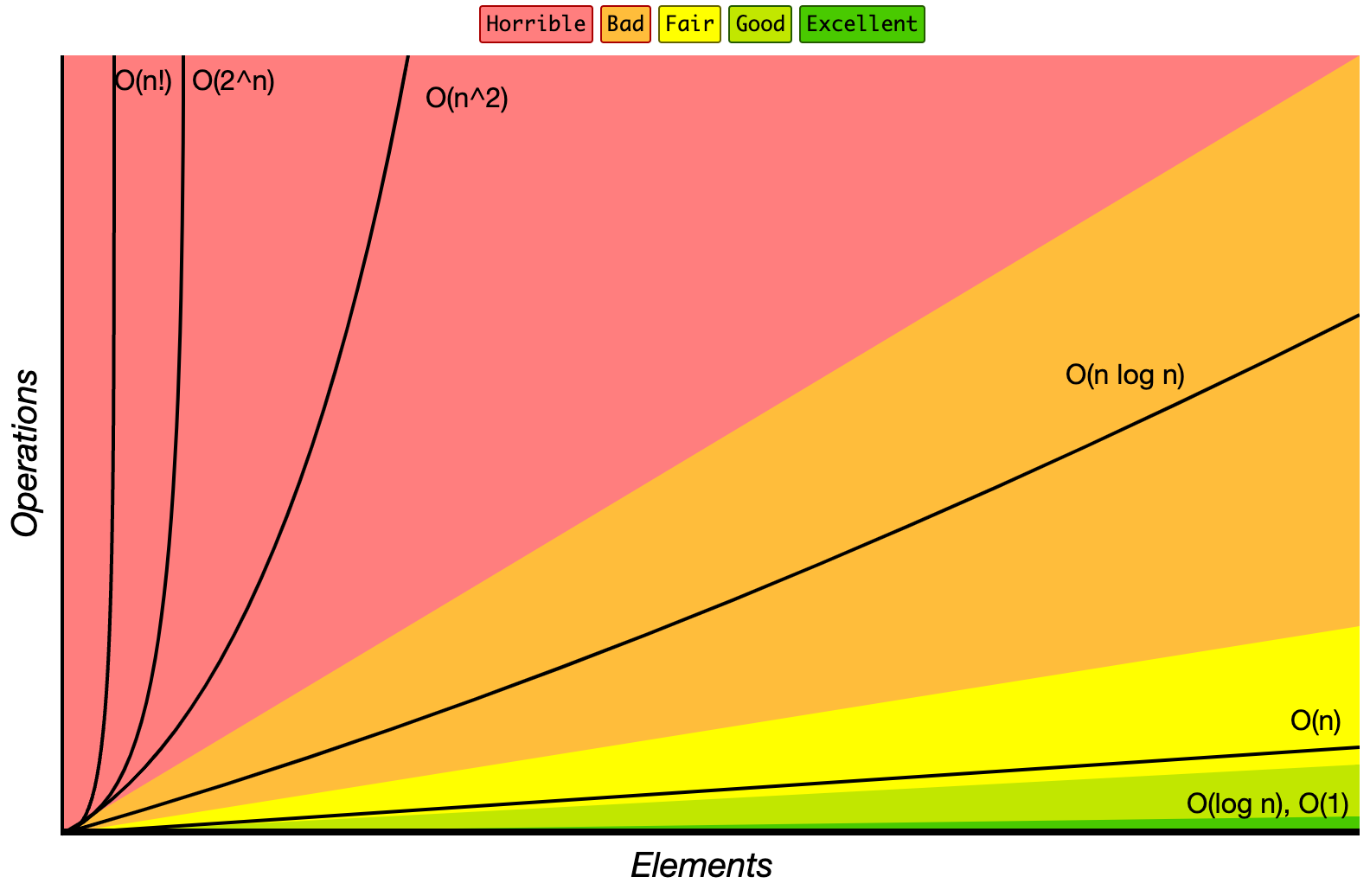 Big-O Complexity chart
from bigocheatsheet
Big-O Complexity chart
from bigocheatsheet
O(1): Constant Time
As you can see, the best-case scenario would be a constant O(1). Let’s say you have a function that returns the first item of a list, something like:
def get_first(n: list):
return n[0]
print(get_first([2,4,6,8,10])) -> 2
It doesn’t matter how big the list gets, since we are only getting the first element, we don’t have to get through the whole array to get it. Some operations in Python also run in O(1) time complexity. A couple of examples would be:
- Append[1]: since the append function only adds one item at the end of a list the function always works in O(1) since it does not depend on iterating over all the objects on the list.
- Get length: the good old methods to grab the length of a list also runs in O(1). Why? At first, I thought it would not make sense since the interpreter would need to go through the list to get the number of values, but Python collections store the number of elements on the list when the item is created or updated without traversing it.
O(n): Linear Time
We can have a scenario where things run smoothly and can do more, they tend to look like O(n). In this case, things run linearly. So as the input grows the time complexity will also grow. A example of that is the solution to FizzBuzz:
def fizz_buzz(n: int):
my_list = []
for i in range(1, n+1):
if i % 3 == 0 and i % 5 == 0:
my_list.append("FizzBuzz")
elif i % 3 == 0:
my_list.append("Fizz")
elif i % 5 == 0:
my_list.append("Buzz")
else:
my_list.append(str(i))
return my_list
print(fizz_buzz(n=100))
As you can see as the input gets bigger the time needed to run will also grow. But in a linear fashion. This happens because we only have one for loop doing the most time-consuming job. So it all depends of the time it will take to get every value from the list with n items. A couple of functions that run in O(n) are:
- Copy: since it is needed to run through all the values on the array.
- Pop an intermediate value: it also needed to run through the elements until reaching the desired value to be popped.
O(n log n)
Entering the realm of your code will take longer and longer to run, we have O(n long). Logarithm scales grow faster than linear. This is common with recursive sorting algorithms and Binary Tree search, it also means that a logarithm operation will occur n times.
In Python, there is one method that takes O(n log n) to run: Sort. Generally speaking, every sorting algorithm takes O(n log n) to run. This is because of the constant permutation between items on the list to find the lowest value and so on. A nice gif from Wikipedia shows the process in action:
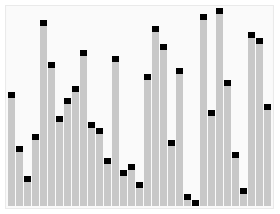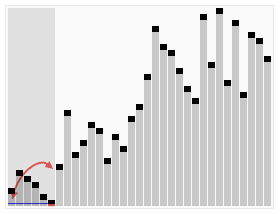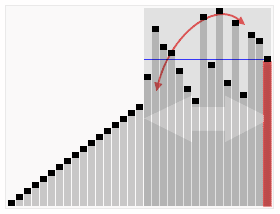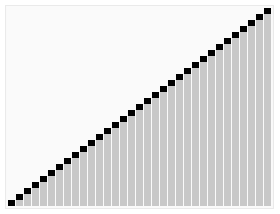
Sort permutation process. Image from:By en:User:RolandH, CC BY-SA 3.0, on Wikipedia
Adding loops to your code will also make it take longer to run.
def double_loop(n: list):
some_list = n.append([,6,7,8,9])
for i in n:
print("Python in nice")
for j in some_list:
print("Hello There!")
return "Nice Job"
print(double_loop([1,2,3,4,5]))
O(n²): Quadratic Time
Quadratic time falls into polynomial complexity and should be considered a red flag. Usually, this happens when we nest loops, so for the quadratic time, we are talking about two nested loops. The exceptions would be if you are working with matrices. An example would be something like the following:
def complex_algo(some_dict: dict):
some_list = []
for i in some_dict.keys():
print("This is a key")
some_list.append(i)
for j in some_dict.values():
print("This is a value")
return some_list
print(complex_algo(some_dict))
Usually, codes that deal with data frames or complex data types show this kind of complexity once that for Data Science, efficiency is not always seen as a priority. No built-in function of Python runs in this type of time complexity as expected. 🙂
O(n!): Factorial Complexity
To wrap up, the worst-case scenario would be O(n!). Factorials, as you may recall, explode really fast as we can recap from the Big-O chart. A cool thing that I read here, exemplifies this complexity by getting a factorial from a deck of cards (52!), this is equivalent to the number of atoms on Earth btw the number is 8.0658175e+67). This also means that the number of ways you can shuffle a deck of cards is pretty much endless, so that deck of cards that you shuffled one-time playing Rummy with your grandma was really unique.
An algorithm that does that is solving the Travelling Salesman Problem by brute force. I’ll come back with more info about that in a separate post, let me know if you are interested 😄
I didn’t cover all the cases here, but if want to know more, feel free to check my ✨fonts✨:
Signin Out o/
